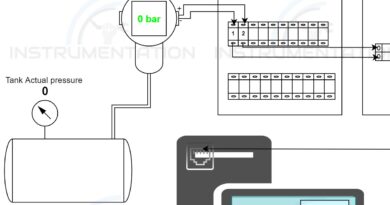
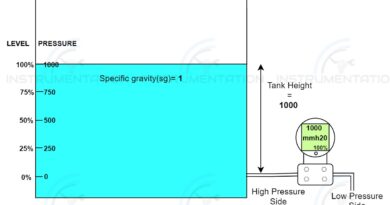
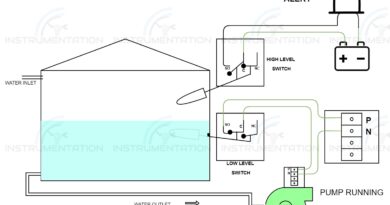
Differential pressure flow transmitter calculation

The flow is directly proportional to the differential pressure(fαΔP). So the measured linear variable from the transmitter has to be converted into a square root in order to obtain a flow value. This example will help you to understand the conversion process taking place.

The Differential pressure transmitter of range 0 to 500 kpa is displaying 100 kpa. And the scaled flow range is 0 to 100m3/hr. What will be the current flow value?

   

 SPAN=URV-LRV  

PV    = 100       LRV=0    URV  =500     SPAN =150

   

 

   

   

Now we got the linear mA in order to obtain a flow rate the linear mA has to be converted into a Square root mA. If you directly use the linear milliamps to calculate the flow rate then you will get the wrong flow rate. so make sure you’re using square root milliamps to obtain a correct flow rate.

You may be familiar with linear to the square root calculation shown below.

   

   

Now we know the square root mA. Now we can easily find the output flow rate by the same formula used initially.

PV    = ?          LRV=0       URV  =100     SPAN =100     mA=11.152

   

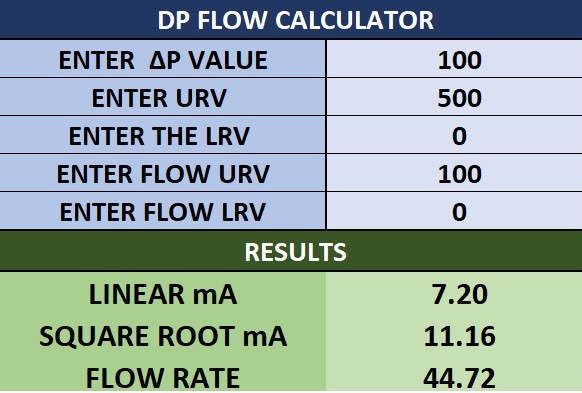
Use above calculator to check the flow rate for the know ΔP value.